PLYWOOD INCLINED BEAM CAPACITY CHECK

BS 5268-2:2002

1.0 INPUT DATA

1.1 Geometrical Properties

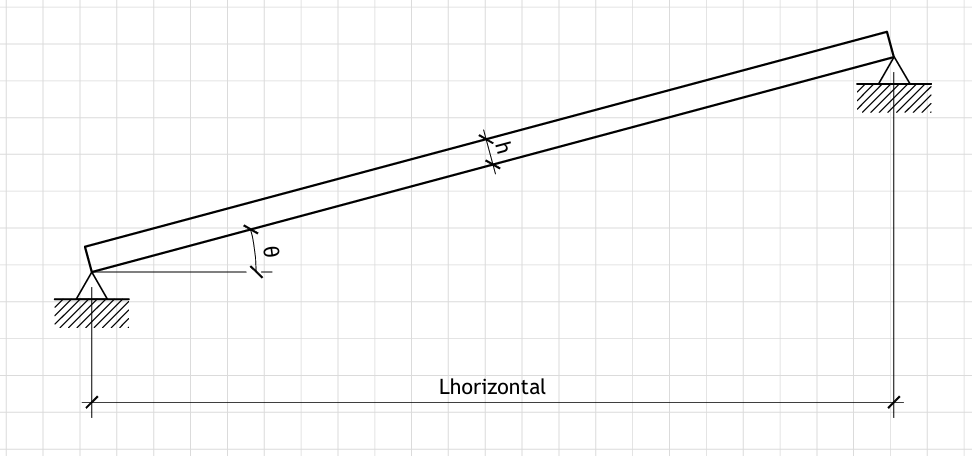
Span (horizontal projection) L_horizontal = mm

Plywood Thickness h = mm

Plywood Width b = mm

Angle of inclination θ = deg

Figure 1: Geometry

Plywood inclined at angle θ with horizontal span L_horizontal

Effective Span along the inclined length L_eff,inclined = L_horizontal/cos(θ)

L_eff,inclined = 380/cos(54°) = 646.15 mm

1.2 Loading

Uniformly Distributed Load (UDL) q_LL = kPa

Total UDL on specified width w_vert = q_LL×b/1000

w_vert = 2×1000/1000 = 2.00 kN/mm

Concentrated Load (mid-span) P_L,LL = kN

1.3 Material Properties (BS 5268-2:2002)

Characteristic Bending Stress f_m,g = N/mm²

Characteristic Shear Stress f_v,g = N/mm²

Characteristic Compression Stress f_c,g = N/mm²

Mean Modulus of Elasticity E_mean = N/mm²

Minimum Modulus of Elasticity E_min = N/mm²

1.4 Modification Factors

Load Duration Factor K₃ =

Depth Factor K₇ =

Load Sharing Factor K₈ =

Compression Factor K₂₂ =

2.0 CALCULATIONS

2.1 Section Properties

Section Area A = b×h

A = 1000×12 = 12000.00 mm²

Second Moment of Area I = (b×h³)/12

I = 1000×12³/12 = 144000.00 mm⁴

Section Modulus Z = (b×h²)/6

Z = 1000×12²/6 = 24000.00 mm³

2.2 Load Resolution into Components

Resolve loads into components normal to and along the beam

UDL perpendicular to beam w_perp = w_vert×cos(θ)

w_perp = 2.00×cos(54°) = 1.18 kN/mm

UDL parallel to beam w_parallel = w_vert×sin(θ)

w_parallel = 2.00×sin(54°) = 1.62 kN/mm

Concentrated load perpendicular to beam P_L,perp = P_L,LL×cos(θ)

P_L,perp = 1.5×cos(54°) = 0.882 kN

Concentrated load parallel to beam P_L,parallel = P_L,LL×sin(θ)

P_L,parallel = 1.5×sin(54°) = 1.214 kN

2.3 Applied Actions

Maximum Bending Moment

M_UDL = w_perp×L_eff,inclined²/8

M_UDL = 1.18×646.15²/8 = 61606.96 kN.mm

M_PL = P_L,perp×L_eff,inclined/4

M_PL = 0.882×646.15/4 = 142.55 kN.mm

Maximum Bending Moment M_max = max(M_UDL; M_PL)

M_max = max(61606.96; 142.55) = 61606.96 kN.mm

Maximum Shear Force

V_UDL = w_perp×L_eff,inclined/2

V_UDL = 1.18×646.15/2 = 381.43 kN

V_PL = P_L,perp/2

V_PL = 0.882/2 = 0.441 kN

Maximum Shear Force V_max = max(V_UDL; V_PL)

V_max = max(381.43; 0.441) = 381.43 kN

Maximum Axial Force (Compression)

N_max = w_parallel×L_eff,inclined + P_L,parallel

N_max = 1.62×646.15 + 1.214 = 1047.04 kN

2.4 Serviceability Check: Deflection

E_deflection = E_mean×K₉ (assuming K₉ = 1.0)

E_deflection = 5800×1.0 = 5800.00 N/mm²

Bending deflection from UDL δ_b,UDL = 5×w_perp×L_eff,inclined⁴/(384×E_deflection×I)

δ_b,UDL = 5×1180.00×646.15⁴/(384×5800.00×144000.00) = 8.44 mm

Bending deflection from PL δ_b,PL = P_L,perp×L_eff,inclined³/(48×E_deflection×I)

δ_b,PL = 882.00×646.15³/(48×5800.00×144000.00) = 0.06 mm

Maximum bending deflection δ_b,max = max(δ_b,UDL; δ_b,PL)

δ_b,max = max(8.44; 0.06) = 8.44 mm

Permissible deflection δ_adm = L_eff,inclined/90

δ_adm = 646.15/90 = 7.18 mm

Deflection Check = FAIL (δ_b,max = 8.44 > δ_adm = 7.18 mm)

2.5 Strength Check: Bending

Permissible bending stress σ_m,adm = f_m,g×K₃×K₇×K₈

σ_m,adm = 6×1.25×1.00×1.00 = 7.50 N/mm²

Applied bending stress σ_m,app = M_max/Z

σ_m,app = 61606.96×1000/24000.00 = 2567.0 N/mm²

Bending Check = FAIL (σ_m,app = 2548.08 > σ_m,adm = 7.50 N/mm²)

2.6 Strength Check: Shear

Permissible shear stress τ_adm = f_v,g×K₃×K₈

τ_adm = 0.5×1.25×1.00 = 0.63 N/mm²

Applied shear stress τ_app = 1.5×V_max/A

τ_app = 1.5×381.43×1000/12000.00 = 47.68 N/mm²

Shear Check = FAIL (τ_app = 47.47 > τ_adm = 0.63 N/mm²)

2.7 Strength Check: Axial Compression

Permissible compression stress σ_c,adm = f_c,g×K₃×K₂₂×K₈

σ_c,adm = 6×1.25×1.00×1.00 = 7.50 N/mm²

Applied axial compression stress σ_c,app = N_max/A

σ_c,app = 1047.04×1000/12000.00 = 87.25 N/mm²

Axial Check = FAIL (σ_c,app = 87.17 > σ_c,adm = 7.50 N/mm²)

2.8 Combined Bending and Compression Check

Interaction ratio = (σ_m,app/σ_m,adm) + (σ_c,app/σ_c,adm)

Interaction ratio = (2567.0/7.50) + (87.25/7.50) = 353.90

Combined Stress Check = FAIL (Interaction ratio = 353.90 > 1.0)

* OUTPUT SUMMARY *

Verification Results

Deflection Check: FAIL

Bending Stress Check: FAIL

Shear Stress Check: FAIL

Axial Stress Check: FAIL

Combined Stress Check: FAIL

Detailed Results

Section Area A = 12000.00 mm²

Second Moment of Area I = 144000.00 mm⁴

Section Modulus Z = 24000.00 mm³

Maximum Bending Moment M_max = 61606.96 kN.mm

Maximum Shear Force V_max = 381.43 kN

Maximum Axial Force N_max = 1047.04 kN

Maximum Deflection δ_b,max = 8.44 mm

RESULTS

DESIGN FAILS - ADDITIONAL STRENGTH OR REINFORCEMENT REQUIRED